Can AI-Generated Text be Reliably Detected?

By O Pilgrim
Translation

image-20230728155956594

arxiv，Github

前言

主要动机是对现有的 AI 生成内容检测器 进行攻击，包括paraphrasing attacks，recursive paraphrasing attacks 和 spoofing attacks，攻击对象包括 neural network-based detectors， zero-shot classifiers，retrieval-based detectors，watermarking techniques

另外，还提出了一个 impossibility result 理论，表明随着模型更复杂、模仿人类的能力更增强，任何检测器的性能一定会随之下降

。。。

[28,29,30]三篇论文貌似也是支撑本文观点的，可能是攻击文章，可以关注

Generalizability: 第二段，[34]提到，因为模型用的是伪随机分布，即狄拉克$δ$函数分布的集合，而人类极不可能生成与任何$δ$函数对应的样本。这意味着人类和人工智能生成的伪随机分布之间的总差异几乎为1，理论上可能存在近乎完美的检测器。不过这并不意味着在有界的计算范围内，这种检测器是存在的

2 Evading AI-Detectors using Paraphrasing Attacks

2.1 Paraphrasing Attacks on Watermarked AI-generated Text

这边针对 Green List 那篇水印文章进行转述攻击，攻击目标是从LLM的输出中删除水印签名。

  • 用来生成水印的模型是OPT-1.3B[8]，并使用大量数据上训练，做文本补全任务。（数据集？？
  • 转述攻击模型有两个，一个是 T5-based[9] paraphrasing model[32]（222M参数量），另一个是 PEGASUS-based[31] paraphrasing model（568M参数量）。都只针对释义任务进行微调。（数据集？？
  • 使用 Extreme Summarization (XSum) [35] 数据集的（某？）100个段落进行评估

攻击过程：

  • OPT-1.3B会生成一部分带水印的文本，然后转述模型逐句接收这些带水印的LLM文本并输出转述后的LLM文本
  • Xsum的文本也会输入OPT-1.3B 来得到另一部分带水印的文本

结果：

  • Table1：PEGASUS-based paraphraser将水印文本中绿色列表标记的百分比从58%（转述前）降低到44%（转述后），检测器的准确率从97%下降到80%，而困惑分数仅为3.5

    image-20230801140618317

  • Table2：展示了转述前后OPT-1.3B输出的带水印文本。这边使用 T5-based paraphraser[32]的目的是要说明，即使是naïve的转述模型也可以将检测器的准确率从97%降至57%

    image-20230801134742845

  • Figure2：显示了检测精度和 T5-based paraphraser 输出文本质量（使用困惑分数测量）之间的权衡。然而，必须指出，困惑度只是评估文本质量的代理指标，因为它的计算依赖于另一个LLM。这里使用更大的 OPT-2.7B[8] 来计算困惑度分数

  • Figure3：使用 DIPPER[4] 进行递归转述攻击。DIPPER将$S$修改为$f(S)$，其中$f$是DIPPER paraphraser。$ppi$指的是第$i$次递归转述。例如，用$f$表示$S$的$pp3$得到$f(f(f(S)))$

    image-20230801140831362

  • Table3：展示了一个 recursively paraphrasing 的样例。在递归转述攻击中，本文使用来自XSum的100个人工书写段落和100个带水印的XSum补全段落来评估ROC曲线。在假阳性率为1%的情况下，经过五轮递归释义后，水印模型的真阳性率从99%（no attack）下降到15% （pp5）。检测器的AUROC由99.8%下降到67.9%

image-20230801140902811

3 Impossibility Results for Reliable Detection of AI-Generated Text

本节论点：随着语言模型变得更加复杂，AI生成的和人类生成的文本序列分布之间的总变异距离会减少(见第4章)

本节内容：提出理论证明，即使是最好的检测器的性能也会随着模型变得更大更强大而下降；即使两个分布之间有适度的重叠，检测性能对于实际部署来说也可能不够好，并可能导致高误报率。（所以不要依赖检测器）

Metrics：检测器的ROC曲线下面积的上界表示 AI 和人类生成文本的分布之间的总变异距离，随着距离减小，AUROC界限接近1/2，相当于随机分类。

定义：$\mathcal{H}$ 是人类生成的文本的分布，$\mathcal{M}$是AI生成的文本的分布，$\Omega$是所有可能文本序列的集合；$TV(\mathcal{M, H})$ 表示两种分布之间的总变异距离；$D:\Omega \to \mathbb{R}$ 是表示detector的function，将文本映射成分值，然后用阈值 $\gamma$ 来分类；通过调整 $\gamma$ 来调整检测器对文本的敏感程度，得到ROC曲线

定理1，任意检测器$D$的ROC曲线下的面积为：

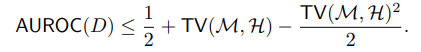
image-20230731152350449

证明：ROC是真阳性率(TPR)和假阳性率(FPR)之间的曲线图，其定义如下：

image-20230731093354688

其中 $\gamma$ 是某个分类器参数。我们可以通过$\mathcal{M}$和$\mathcal{H}$之间的总变化来限定$TPR_{\gamma}$和$FPR_{\gamma}$之间的差异：

image-20230731093410584

由于$TPR_{\gamma}$也受$1$限制，则：

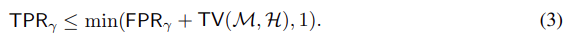
image-20230731094356389

为简洁起见，用$x$, $y$和$tv$表示$FPR_{\gamma}$， $TPR_{\gamma}$和$TV(\mathcal{M, H})$，则 AUROC 计算如下：

image-20230731094614225

图7显示了上述边界作为总变化的函数是如何增长的。对于具有良好性能的检测器(例如AUROC≥0.9)，人类和人工智能生成的文本的分布必须彼此非常不同(总变异>0.5)。当两个分布变得相似时(例如，总变化≤0.2)，即使是最好的检测器的性能也不好(AUROC <0.7)。这表明，区分由非水印语言模型生成的文本和人类生成的文本是一项根本困难的任务。需要注意的是，对于一个加了水印的模型，由于加了水印的分布与人为生成的分布之间的总变异距离可能很大，所以上述边界可以接近于$1$。接下来，我们将讨论释义攻击在这种情况下是如何有效的。

image-20230731141445022

3.1 Paraphrasing to Evade Detection

虽然我们的分析考虑了所有人类和一般语言模型生成的文本，但通过适当地定义$\mathcal{M}$和$\mathcal{H}$，它也可以应用于特定的场景，例如特定的写作风格或句子释义。例如，它可以用来证明人工智能生成的文本，即使带有水印，也可以通过简单地将其传递给释义工具而难以检测。考虑一个释义器，它将AI模型生成的序列作为输入，并产生具有类似含义的类人类的序列。设$\mathcal{M=R_M}(s)$和$\mathcal{H=R_H}(s)$分别为释义器和人类产生的与$s$意义相近的序列的分布。释义器的目标是使其分布$\mathcal{R_M}(s)$尽可能地与人类分布$\mathcal{R_H}(s)$相似，从本质上减少它们之间的总变化距离。定理1为检测器$D$的性能设定了以下界限，检测器$D$试图从人类产生的序列中检测释义器的输出。

推论1，检测器$D$的ROC下的面积为：

image-20230731095421083

真阳性率和假阳性率之间的一般权衡。理解人工智能生成的文本检测器的局限性的另一种方法是直接通过描述真阳性率和假阳性率之间的权衡。根据不等式$2$，我们有以下推论：

推论2，对于任意水印方案$W$：

image-20230731101142582

其中$\mathcal{R_M}(s)$和$\mathcal{R_H}(s)$分别是由释义模型和人类产生的$s$的复述序列的分布。

人类可能有不同的写作风格。推论2表明，如果复述模型类似于某些人类文本分布$\mathcal{H}$(即$TV(\mathcal{R_M}(s), \mathcal{R_H}(s))$较小)，则某些人的写作将被错误地检测为水印(即$Pr_{s_w} \thicksim \mathcal{R_H}(s) [s_w使用W进行水印]$的值高)，或者复述模型可以去除水印(即$Pr_{s_w} \thicksim \mathcal{R_M}(s) [s_w使用W进行水印]$的值低)。

推论3，对于任意 AI文本检测器$D$，

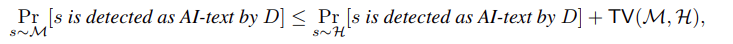
image-20230731103126990

其中$\mathcal{M}$和$\mathcal{H}$分别表示模型和人类的文本分布。

推论3表明，如果一个模型类似于某些人类文本分布$\mathcal{H}$(即$TV(\mathcal{M, H})$很小)，那么某些人的写作将被错误地检测为人工智能生成的文本(即$Pr_{s \thicksim \mathcal{H}}[s被D检测为人工智能文本]$很高)，或者人工智能生成的文本将无法被可靠地检测出来(即$Pr_{s \thicksim \mathcal{M}}[s被D检测为人工智能文本]$很低)。

这些结果证明了人工智能文本检测器的基本局限性，无论是否使用水印方案。在附录3.2中，我们给出了定理1中界的紧密性分析，其中我们证明了对于任何人类分布$\mathcal{H}$，存在一个AI分布和一个检测器$D$，对于该分布，界是相等的。

3.2 Tightness Analysis

本节中，我们证明定理1中的界是紧的。对于任意两个分布$\mathcal{H}$和$\mathcal{M}$，例如，在一维中移动了一段距离的两个相同的正态分布，这个界不必是紧的。然而，对于每个人类分布$\mathcal{H}$，紧密性都可以表现出来。对于人类生成的文本序列$\mathcal{H}$的给定分布，我们构建了一个人工智能文本分布$\mathcal{M}$和一个检测器$D$，使得边界相等。

定义人工生成文本$pdf_{\mathcal{H}}$在所有序列$\Omega$上分布的概率密度函数的子水平集如下：

image-20230731111314714

式中$c \in \mathbb{R}$，设$\Omega_{\mathcal{H}}(0)$不为空。现在，考虑一个密度函数为$pdf_{\mathcal{M}}$的分布$M$，它具有以下性质:

  1. 从$\mathcal{M}$抽取的序列落在$\Omega_{\mathcal{H}}(0)$中的概率为$TV(\mathcal{M}, \mathcal{H})$，即：$\mathbb{P_s \thicksim \mathcal{M}}[s \in \Omega_{\mathcal{H}}(0)] = TV(\mathcal{M, H})$
  2. 对于所有$s \in \Omega(\tau) - \Omega(0)$且$\tau > 0$，令$pdf_{\mathcal{M}}(s) = pdf_{\mathcal{H}}(s)$，使得$\mathbb{P}_{s \thicksim \mathcal{H}}[s \in \Omega(\tau)] = 1-TV(\mathcal{M, H})$
  3. 对于所有$s \in \Omega - \Omega(\tau)$，有$pdf_{\mathcal{M}}(s)=0$

定义一个假设的检测器$D$，将$\Omega$中的每个序列映射到$\mathcal{H}$的概率密度函数的负值，即$D(s) = - pdf_{\mathcal{H}}(s)$。利用$TPR_{\gamma}$和$FPR_{\gamma}$的定义，我们有:

image-20230731112350342

类似的，

image-20230731112415152

对于$\gamma \in [-\gamma, 0]$，

image-20230731112504699

对于$\gamma \in [-\infty, -\gamma]$，根据性质3，$TPR_{\gamma} = 1$。同样，当$\gamma$从$0$到负无穷，$FPR_{\gamma} = 1$从$0$到$1$。因此，$TPR_{\gamma} = min(FPR_{\gamma} + TV(\mathcal{M}, \mathcal{H})， 1)$，与式3相似。以与前一节类似的方式计算AUROC，我们得到以下结果:

image-20230731112900718

3.3 Pseudorandomness in LLMs

大多数机器学习模型，包括大型语言模型(llm)，以一种或另一种形式使用伪随机数生成器来产生它们的输出。例如，LLM可以使用伪随机数生成器对输出序列中的下一个令牌进行采样。在讨论我们的不可能结果时，Kirchenbauer等人[34]在最近的一项工作中认为，这种伪随机性使得人工智能生成的文本分布与人类生成的文本分布非常不同。这是因为人工智能生成的伪随机分布是狄拉克$δ$函数分布的集合，而人类极不可能生成与任何$δ$函数对应的样本。在我们的框架中，这意味着人类和伪随机人工智能生成的分布之间的总变化几乎是$1$，使得定理1中的界是空的。

我们认为，尽管人类和伪随机人工智能生成的分布之间的真实总变化很大，并且存在(理论上)可以几乎完美地分离分布的检测器函数，但该函数可能无法有效计算。任何多项式时间可计算的检测器都只能从伪随机而不是真随机中获得微不足道的优势。如果我们知道用于伪随机数生成器的种子，我们就能够预测伪随机样本。然而，一个试图逃避检测的人可以简单地随机分配这个种子，这使得预测样本在计算上是不可行的。

我们修改定理1中的界，以包含一个可忽略不计的校正项，以解释伪随机性的使用。我们证明了多项式时间可计算检测器$D$在人工智能生成的分布$\widehat{\mathcal{M}}$的伪随机版本上的性能由真正随机分布$\mathcal{M}$(由使用真随机性的LLM产生)的总变化有界，如下所示：

image-20230731113133653

项$\epsilon$表示$\mathcal{M}$和$\widehat{\mathcal{M}}$赋给任意多项式时间可计算的${0,1}$函数$f$的概率之差，即:

image-20230731113239229

这一项比边界中的任何一项都小几个数量级，可以安全地忽略。例如，对于正整数$t$，常用的伪随机发生器可以实现$\epsilon$，它受限于一个可以忽略不计的函数$1/b^t$，其中$b$是发生器种子中使用的比特数[37,38]。从计算的角度来看，伪随机分布的总变异与人工智能生成的真正随机分布几乎相同。因此，我们的框架为现实世界的LLMs提供了一个合理的近似值，即使在存在伪随机性的情况下，不可能结果也成立。

计算总变异距离：正如两个概率分布之间的总变异距离$TV$被定义为两个分布分配给任意{0,1}-函数的概率之差，我们为多项式时间可计算函数定义了这个距离$TV_c$的计算版本：

image-20230731122117728

其中$\mathcal{P}$表示多项式时间可计算{0,1}-函数的集合。$\mathcal{P}$也可以定义为所有 polynomial-size circuits的集合，这更适合于基于深度神经网络的检测器。函数$f$可以认为是检测参数大于某一阈值的指示函数，即定理1证明中的$D(s)≥γ$。以下引理适用于多项式时间检测器$D$的性能:

引理1，任意多项式时间可计算检测器$D$的ROC下的面积有界为：

image-20230731122542028

该引理的证明方法与定理1相同，即将真随机生成分布$\mathcal{M}$替换为其伪随机版本$\widehat{\mathcal{M}}$，将真总变分$TV$替换为其计算变体$TV_c$。

接下来，我们将$\mathcal{H}$与伪随机分布$\widehat{\mathcal{M}}$之间的计算总变化$TV_c$与$\mathcal{H}$与真随机分布$\mathcal{M}$之间的总变化$TV$联系起来。

引理2，对于人类分布$\mathcal{H}$，人工智能生成的真正随机分布$\mathcal{M}$及其伪随机版本$\widehat{\mathcal{M}}$，

image-20230731122917202

这表明，虽然由于伪随机性的存在，真实的总变异可能会很高，但有效的总变异仍然很低。现在我们用它来证明不可能结果的修正版本。

定理2(计算不可能结果)，任意多项式时间可计算检测器$D$对$\mathcal{H}$和伪随机分布$\widehat{\mathcal{M}}$的AUROC用真随机分布$\mathcal{M}$的$TV$有界

image-20230731123123926

image-20230731123141972

4 Estimating Total Variation between Human and AI Text Distributions

我们估计了人类文本分布(WebText)和OpenAI GPT-2系列中几个模型的输出分布之间的总变化($TV$)对于两个分布$\mathcal{H}$和$\mathcal{M}$，它们之间的总变异定义为它们在样本空间$Ω$上对任意事件$E$分配的概率之差的最大值，即:

image-20230731123308529

因此，对于任何事件$E$，这个概率差是两个分布之间总变化的有效下界。由于我们不知道$\mathcal{H}$和$\mathcal{M}$的概率密度函数，因此在整个事件空间上解决上述最大化问题是棘手的。因此，我们将事件空间近似为一类由神经网络定义的事件，该神经网络具有参数$θ$，将$Ω$中的文本序列映射为实数。当神经网络的输出高于阈值$τ$时，相应的事件$θ$发生。我们试图找到一个事件$E_θ$，它能得到总变分的一个尽可能紧的下界。

估计过程：我们在人类和人工智能文本分布的样本上训练了一个RoBERTa大型分类器[17]。给定一个文本序列，这个分类器产生一个$0$到$1$之间的分数，表示模型认为该序列是人工智能生成的可能性有多大。假设AI文本分布为正类，我们为该分数选择一个阈值，该阈值使用验证集中的样本将真阳性率(TPR)和假阳性率(FPR)之间的差值最大化。最后，我们将总变异估计为测试集上TPR和FPR之间的差异。这种差异本质上是人类和ai生成的文本分布分配给上述分类器的概率之间的差距，用于计算阈值，这是总变化的下界。

图8绘制了使用RoBERTa-large架构估计的四种不同文本序列长度(25、50、75和100)的四种GPT-2模型(小、中、大和XL)的总变化估计。我们为每个GPT-2模型和序列长度训练该架构的单独实例，以估计相应分布的总变化。我们观察到，随着模型变得更大更复杂，人类和人工智能文本分布之间的电视估计减少。这表明，随着语言模型变得越来越强大，它们的输出分布与人类生成的文本分布之间的统计差异消失了。

image-20230731125244024

4.1 Estimating Total Variation for GPT-3 Models

我们使用OpenAI平台上的GPT-3系列模型Ada、Babbage和Curie重复上述实验，我们使用WebText和ArXiv摘要[39]数据集作为人类文本分布。在以上三个模型中，Ada在文本生成能力方面是最不强大的，而Curie是最强大的。由于这些模型的输出没有免费可用的数据集，因此我们使用OpenAI的API服务来生成所需的数据集。

我们将WebText中的每个人类文本序列拆分为“prompt”和“completion”，其中prompt包含原始序列的前100个标记，completion包含其余的标记。然后，我们在OpenAI API中使用温度设置为0.4的GPT-3模型使用提示生成完井。我们使用这些模型补全和人类文本序列的“补全”部分，以与第4节相同的方式使用RoBERTa-large模型来估计总变化。使用人类序列的前100个标记作为提示，允许我们控制生成文本的上下文。这使我们能够在相同的上下文中比较生成的文本与人类文本的相似性。

图9a绘制了GPT-3模型相对于WebText的四种不同序列长度25、50、75和100的总变化估计。与§4中的GPT-2模型相似，我们观察到最强大的模型Curie在所有序列长度上的总变异最小。然而，Babbage模型没有遵循这一趋势，甚至比最弱的Ada模型显示出更高的总变化。

考虑到WebText包含来自广泛的Internet数据源的数据，我们还尝试了更集中的场景，例如为科学文献生成内容。我们使用ArXiv抽象数据集作为人类文本，并估计上述三种模型的总变化(图9b)。我们观察到，对于大多数序列长度，总变异在Ada、Babbage和Curie系列模型中减小。这进一步证明，随着语言模型能力的提高，它们的输出与人类文本越来越难以区分，这使得它们更难被检测到。

image-20230731125511682

5 Spoofing Attacks on AI-text Generative Models

5.1 Spoofing Attacks on Watermarked Models

在Kirchenbauer等人[1]中，他们通过断言模型输出具有某些特定模式的token来为LLM输出加水印，这些模式可以很容易地以极低的错误率检测到。软水印文本主要由 green list tokens 组成。如果攻击者能够了解软水印方案的 green list，他们就可以使用这些信息对人工编写文本进行处理使其被检测为带水印文本。实验表明，该软水印方案可以有效地欺骗。虽然软水印检测器可以非常准确地检测到水印的存在，但无法确定该模式是由人类还是LLM生成的。攻击者可以以这种方式编写贬损的带水印文本，这些文本被检测到是带水印的，这可能会对带水印的LLM的开发人员造成声誉损害。因此，研究欺骗攻击以避免此类情况的发生是非常重要的。

在水印中，前缀单词$s ^{(t−1)}$决定了用于选择单词$s ^{(t)}$的 green list。攻击者的目标是为词汇表中$N$个最常用的单词计算 green list 的代理。我们在实验中使用$N = 181$，这是一个相对较小的值。攻击者查询带水印的OPT-1.3B[8] 106次，观察其输出中成对出现的token，以估计$N$个 tokens 的 green list score。前缀$s ^{(t)}$的 green list score 较高的 token 可能位于其 green list 中（参见图10）。我们建立了一个工具，通过向攻击者提供代理 green list 来帮助他们创建带水印的句子。通过这种方式，我们可以很容易地欺骗水印模型。如表5所示，是由一个敌对的人类创造的句子。图11显示，在 paraphrasing and spoofing 攻击的情况下，基于水印的检测器的性能显著下降，表明它们不可靠

image-20230801144104669

image-20230801144205986

image-20230801143248755