
ABSTRACT
最近,人们提出了各种探测任务,以发现在语境化词嵌入中学习到的语言属性。这些工作中的许多隐含假设这些嵌入位于某些度量空间中,通常是欧几里得空间。本文考虑了一类几何特殊空间,即双曲空间,对层次结构表现出更好的归纳偏差,并可能更好地揭示在上下文表示中编码的语言层次。本文提出庞加莱探针,一种结构探针,将这些嵌入投影到具有明确定义的层次结构的庞加莱子空间。本文关注两个探索目标:(a)依存树,其中层次结构被定义为头部依赖结构;(b)词汇情感,层次被定义为单词的极性(积极和消极)。我们认为,一个探针的关键要求是它对语言结构存在的敏感性。将该探测应用于BERT,这是一种典型的上下文嵌入模型。在句法子空间中,该探针比欧几里得探针更好地恢复了树结构,揭示了BERT语法的几何形状不一定是欧几里得的可能性。在情感子空间中,揭示了积极和消极情感的两种可能的元嵌入,并展示了词汇控制的语境化如何改变嵌入的几何定位。通过广泛的实验和可视化,用庞加莱探针展示了这些发现。
1 INTRODUCTION
使用预训练语言模型的语境化单词表示显著推进了NLP的进展(Peters等人,2018a;Devlin et al., 2019)。先前的研究指出,在这些表征中隐含着丰富的语言知识(Belinkov et al., 2017;Peters等,2018b;a;Tenney et al., 2019)。本文的灵感主要来自Hewitt & Manning(2019),他们提出了一种结构探针,用于恢复句法子空间中在平方欧几里得距离下编码的依赖树。虽然这是一个隐含的假设,但没有严格的证据表明这些句法子空间的几何形状应该是欧几里得的,特别是在欧几里得空间对树建模存在内在困难的情况下(Linial et al., 1995)。
我们建议施加和探索不同的 inductive biases 来建模语法子空间。双曲空间是一种具有恒定负曲率的特殊黎曼空间,由于其树状结构(Nickel & Kiela, 2017;Sarkar, 2011)。我们采用广义庞加莱球(一种特殊的双曲空间模型)来构造上下文嵌入的庞加莱探针。图1 (A, B)给出了一个嵌入庞加莱球中的树的例子,并比较了欧几里得对应的树。直观上,庞加莱球的体积随其半径呈指数增长,这类似于一棵满树的节点数随其深度呈指数增长的现象。这将提供“足够的空间”来嵌入树。同时,欧几里得球的体积呈多项式增长,因此嵌入树节点的能力较小。

在进一步讨论之前,区分探测和监督解析器是至关重要的(Hall Maudslay et al., 2020),并询问什么是好的探测。理想情况下,探测应该正确地恢复嵌入中包含的语法信息,而不是本身就是一个强大的解析器。因此,探测应该具有有限的建模能力,但仍然对语法的存在足够敏感,这一点很重要。对于没有强语法信息的嵌入(例如,随机初始化的词嵌入),探测不应该以分配高解析分数为目标(因为这会高估语法的存在性),而解析器的目标是获得高分,无论输入嵌入有多糟糕。探针的质量由其对语法的敏感性来定义。
我们在双曲空间中探索BERT的工作是探索性的。与Hewitt & Manning(2019)中的欧几里得句法子空间相反,我们考虑了庞加莱句法子空间,并展示了其在恢复语法方面的有效性。图1(C)给出了嵌入庞加莱球中的重构依赖树的例子。在我们的实验中,我们强调了庞加莱探针的两个重要观察结果:(a)它没有给基线嵌入(没有语法信息)比欧几里得探针更高的解析分数,这意味着它不是一个更好的解析器;(b)与容量受到严格限制的欧几里得探针相比,它显示出更高的解析分数,特别是对于更深的树、更长的边和更长的句子。结果(b)可以从两个角度来解释:(1)它表明庞加莱探测可能对更深层次语法的存在更敏感;(2) BERT的句法子空间结构可能不同于欧几里得,特别是对于更深的树。因此,欧氏探测可能低估了BERT的句法能力,而BERT可能在某些特殊度量空间(在我们的例子中是庞加莱球)中表现出更强的深层语法建模能力。
为了更好地利用双曲空间层次结构的归纳偏差,我们将庞加莱探针推广到情感分析中。我们通过使用向量几何预测单个单词的情感来构建庞加莱情感子空间(图1 D)。我们假设积极和消极情感的两个元表示作为情感子空间的根。一个词的极性越强,它就越接近它对应的元嵌入。在我们的实验中,具有明显不同的几何属性,庞加莱探针显示BERT以非常细粒度的方式为每个单词编码情感。我们进一步揭示了词嵌入的定位如何根据词汇控制的语境化而变化,即不同的语境如何影响嵌入在情感子空间中的几何位置。
总之,我们提出了一个庞加莱探针来揭示在BERT中编码的分层语言结构。从双曲深度学习的角度来看,我们的结果表明使用庞加莱模型来学习更好的语言层次表示的可能性。从语言学的角度来看,我们揭示了BERT编码的语言层次的几何性质,并假设BERT可以在不一定是欧几里得的特殊度量空间中编码语言信息。我们通过大量的实验和可视化来证明我们的方法的有效性。
2 RELATED WORK
Probing BERT:最近,人们对寻找BERT编码的语言信息越来越感兴趣 (Rogers et al., 2020)。一个典型的工作是结构探测,旨在揭示语法树如何在BERT嵌入中进行几何编码 (Hewitt & Manning, 2019;Reif et al., 2019)。我们的庞加莱探索通常遵循这条线,并利用双曲空间的几何特性来建模树木。我们再次注意到,语法探针的目标是找到容量严格受限的语法树,即探针不应该是解析器 (Hewitt & Manning, 2019; Kim et al., 2020),并在实验中严格遵循这一限制。其他探索任务考虑了各种语言属性,包括形态学 (Belinkov et al., 2017)、词义 (Reif et al., 2019)、短语 (Kim et al., 2020)、语义片段 (Richardson et al., 2020)以及语法和语义的其他方面 (Tenney et al., 2019)。我们对情感的庞加莱扩展探针可以被视为一个典型的语义探针,揭示了BERT如何几何编码单词情感。
Hyperbolic Deep Learning:最近,使用双曲几何的方法被提出用于几个NLP任务,因为它在捕获层次信息方面比欧氏空间有更好的归纳偏差。庞加莱嵌入 (Nickel & Kiela, 2017) 和 POINCAREGLOVE (Tifrea et al., 2019) 使用庞加莱模型学习层次的嵌入,并表现出令人印象深刻的结果,特别是在低维度上。这些工作显示了双曲几何在建模树木方面的优势,而专注于使用双曲空间来探测上下文嵌入。为了在双曲空间中学习模型,之前的工作将莫比乌斯陀螺向量空间的形式与黎曼几何相结合,推导出重要数学运算的双曲版本,如莫比乌斯矩阵向量乘法,并使用它们来构建双曲神经网络 (Ganea et al., 2018)。黎曼自适应优化方法 (Bonnabel, 2013; Becigneul & Ganea, 2019) 被提出用于基于梯度的优化。这些工作中的技术被用作训练庞加莱探针的基础设施。
3 POINCARE´ PROBE
我们从回顾双曲几何的基础知识开始。我们遵循 Ganea et al. (2018)。广义庞加莱球是双曲空间的典型模型,表示为$(\mathbb{D}^n_c, g^{\mathbb{D}}_x)$,对于$c>0$,$\mathbb{D}^n_c=$${ x \in \mathbb{R}^n \mid c \parallel x \parallel ^2 < 1 }$是一个黎曼流形,$g^{\mathbb{D}}_x=(λ^c_x)^2 I_n$是度规张量,$λ^c_x=2/(1-c \parallel x \parallel ^2)$是保形因子,$c$是双曲空间的负曲率。我们将根据上下文交替使用术语双曲和庞加莱。我们的庞加莱探针使用标准的庞加莱球$\mathbb{D}^n_c$ with $c=1$。$x,y \in \mathbb{D}^n_c$的距离公式为:
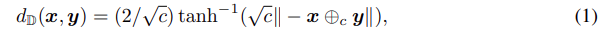
其中$⊕_c$表示莫比乌斯加法,即加法运算符的双曲版本。注意,当$c→0$时,我们恢复了欧几里得空间$\mathbb{R}^n$。此外,我们使用$M ⊗_c x$来表示线性映射$M: \mathbb{R}^n→\mathbb{R}^m$的莫比乌斯矩阵-向量乘法,这是线性变换的双曲版本。我们使用$exp^c_x(·)$来表示指数映射,它将切空间(在我们的例子中,从BERT嵌入空间投影的空间)中的向量映射到双曲空间。它们的闭合公式详见附录C。
该探针由两个简单的线性映射$P$和$Q$组成,将BERT嵌入到庞加莱的语法/情感子空间中。形式上,让$\mathcal{M}$表示一个预训练语言模型,它产生一个分布式表示序列$h_{1:t}$给定一个由t个单词组成的句子$w_{1:t}$。训练一个线性映射$P: \mathbb{R}^n→\mathbb{R}^k$,$n$是上下文嵌入的维数,$k$是探测秩,它将分布式表示投影到切空间。然后指数映射将切空间投影到双曲空间。在双曲空间中,我们通过另一个线性映射$Q: \mathbb{R}^k→\mathbb{R}^k$构建了庞加莱的语法/情感子空间。公式如下:

这里$P$将原始BERT嵌入空间映射到庞加莱球原点的切线空间。然后$exp_0(·)$映射庞加莱球内部的切线空间。因此,在方程3中,我们使用莫比乌斯矩阵向量乘法作为双曲空间中的线性变换。
4 PROBING SYNTAX
根据Hewitt & Manning(2019)的研究,我们的目标是测试是否存在从原始BERT嵌入空间转换为简单参数化的双曲子空间,其中嵌入之间的平方距离或嵌入的平方范数分别近似于树距离或节点深度。探测的目标是恢复嵌入中固有的语法信息。为此,探测不应该给基线的 non-contextualized embeddings 分配很高的解析分数(否则它将成为一个解析器,而不是一个探测)。因此,对于探针来说,具有有限的建模能力(在我们的例子中是两个线性变换$P$和$Q$),但仍然对语法结构足够敏感是至关重要的。我们进一步测试庞加莱探测是否能够在它本身对建模树的固有偏见条件下,发现更深层次树的更多语法信息。
与Hewitt & Manning(2019)类似,我们使用庞加莱距离的平方来重建单词对之间的树距离,使用庞加莱距离的平方来重建单词的深度:

其中$d_T(w_i, w_j)$表示单词$i$、$j$在它们的依赖树上的距离,即单词$i$与$j$连接的边数,$d_D(w_i)$表示单词$i$在依赖树中的深度。为了优化,我们使用Adam (Kingma & Ba, 2014)初始化学习率为0.001,并训练多达40个epoch。我们衰减学习率并根据 dev loss 进行模型选择。
4.1 EXPERIMENTAL SETTINGS
我们的实验旨在证明庞加莱探测可以更好地恢复BERT中更深层次的语法,而无需成为解析器。我们在 Hewitt & Manning (2019) Euclidean probes 中表示探针,并遵循其数据集和主要基线模型。具体来说,我们使用 Penn Treebank数据集(Marcus & Marcinkiewicz, 1993),并重用Hewitt & Manning(2019)中的数据处理代码,将数据格式转换为Stanford Dependency (de Marneffe等人,2006)。对于基线模型,我们使用:
(a) ELMO 0:没有上下文信息的强字符级词嵌入。所有探测都不应该从这些嵌入中找到语法树。
(b) LINEAR:从左到右的结构树,只包含位置信息。
(c) ELMO 1和BERT:具有丰富语法信息的强上下文化嵌入。
所有探测都应该准确地恢复其中编码的所有解析树。
由于探测的目标是在严格的概念中恢复语法树,因此我们将Poincare探测限制为64维,即$P$和$Q$的$k = 64$,这与Hewitt & Manning(2019)中报道的欧氏探测的有效秩相同或更小。我们还强调,我们的庞加莱探针的参数仅仅是两个矩阵,这也明显小于典型的深度神经网络解析器(Dozat & Manning, 2016)。
为了评估树距离探针,我们报告了:(a) undirected unlabeled attachment scores (UUAS),该分数显示未标记的边缘是否被正确恢复,相对于Gold的无向树;(b)distance Spearman Correlation(DSpr),显示恢复距离(欧几里得或双曲)如何与Gold的树距离相关的分数。为了评估树深度探测,我们报告了:(a)norm Spearman Correlation (NSpr),显示真实深度排序与预测深度排序之间的相关性的分数;(b)the corretly identified root nodes (root%),表示探针识别句子词根的程度。
4.2 RESULTS
表1显示了树的距离和深度探测的主要结果。我们看到,对于ELMO 0和LINEAR,庞加莱探测并没有给出比欧几里得探测更高的分数(即,它们不是解析器。另外请参见附录a .1 GRU如何将探针转换为解析器),并在深度上下文化的嵌入中恢复更高的解析分数。结果表明:(a)庞加莱探针可能对句法信息的存在更为敏感;(b)由于欧几里得探针无法对树进行建模,因此可能低估了语境化嵌入中编码的语法信息。我们进一步从多个角度详细分析了这两种探测器的距离任务,这比深度任务更难。

Different BERTBASE Layers: 图2A报告了在BERTBASE的每一层上训练的Poincae探针和Euclidean探针的距离分数。两者是一致的,表现出语法主要存在于中间层的相似趋势。
Probe Rank:图2B报告了BERTBASE7中不同$k$级探针的距离分数。与Hewitt & Manning(2019)类似,我们看到庞加莱探针在64维之后得分没有增加。我们假设可能存在一些维数接近64的内在句法子空间,但将进一步的研究留给未来的工作。
Sentence and Edge Lengths: 图2C报告了BERTBASE7中不同长度句子的距离分数。结果,庞加莱探针在较长的句子中比欧几里得探针得分更高,这意味着它们能更好地重建更深层次的语法。图3(Left)分别比较了欧几里得探针和庞加莱探针预测的边缘与Gold真值边缘之间的边缘距离(长度)分布。从庞加莱探测器得到的分布更接近于真实分布,特别是对于较长的树。图3(Right)显示,对于平均长度较长的边缘类型,庞加莱探针始终能够获得更好的召回率。附录中的图11进一步比较了在BERTBASE7上通过预测平方距离得到的最小生成树结果(我们从开发集中随机抽取12个实例)。从语言学的角度来看,这些观察结果特别有趣,因为长句子的句法结构比短句子的句法结构更复杂,也更有挑战性。一个很有希望的未来方向是使用双曲空间进行解析。
Curvature of the Hyperbolic Space:我们进一步用曲率参数表征双曲句法子空间的结构,曲率参数测量空间的“弯曲”程度(图2D)。我们看到最优曲率大约是$-1$,这是一个标准庞加莱球的曲率。此外,如果我们逐渐将曲率改为$0$,空间将“不那么弯曲”,更类似于欧几里得空间(更“平坦”)。因此,庞加莱分数收敛于欧几里得分数。当曲率为$0$时,我们恢复欧几里得探针。


Visualization of Syntax Trees:为了说明欧几里得和庞加莱语法子空间之间的结构差异,我们在图4中可视化了恢复的依赖树。为了同时可视化边缘和树深度,我们对方程4和5中的两个探测目标进行了联合训练。然后使用PCA投影来可视化语法树,类似于Reif et al. (2019)。如图4所示,与欧几里得探针相比,庞加莱探针显示出更有组织的单词层次结构:词根day位于原点,并根据树的深度被其他单词包围。我们进一步注意到,ELMO 0的嵌入不包含语法信息,相应的树看起来毫无意义。

4.3 SUMMARY ON SYNTACTIC PROBE
BERT嵌入的流形可能是复杂的,并表现出特殊的几何性质。我们的探针本质上作为一个定义良好的、可微的、满射函数,将BERT嵌入空间映射到一个低维的、适度弯曲的庞加莱球(而不是欧几里得空间),从而导致更好的语法树重建。这表明BERT语法的流形可能在几何上更类似于庞加莱球而不是欧几里得空间。当然,我们不能断定句法子空间确实是双曲的。比起总结结论,我们的目标是探索BERT语法的替代模型,并揭示潜在的几何结构。BERT的这些几何性质还远远没有被很好地理解,仍然有许多开放的问题值得研究。
5 PROBING SENTIMENT
在验证了重建庞加莱探针的语法树的有效性之后,在本节中,我们将探针推广到语义层次结构并专注于情感。我们首先恢复一个庞加莱情感子空间,其中两个元正嵌入和元负嵌入采用最顶层的层次结构,然后在该子空间中识别单词定位。我们强调,我们的探针揭示BERT为每个单词编码细粒度的情感(积极,消极和中性),即使探针是用句子级二进制标签训练的。为了进一步研究句子的上下文如何影响其词嵌入,我们进行了定性的词汇控制语境化,即根据常见的语言规则通过仔细改变词的选择来改变句子的情绪,并可视化嵌入的本地化如何相应变化。
我们使用与第3节中描述的相同的探测架构来构建情感子空间。同样,探针由两个矩阵$P$和$Q$参数化,它们将BERT嵌入投影到庞加莱球中。我们采用句子的情感标签作为监督信号,并使用具有简单二元标签(正面和负面)的Movie ‘ Review数据集(Pang & Lee, 2005)。该数据集的详细信息见附录b。给定一个有$t$个单词$w_{1:t}$的句子,我们根据方程2和3对其BERT嵌入进行投影,得到$q_i \in \mathbb{D}^k$。为了从矢量几何的角度解释分类过程,我们为正标签和负标签设置了两个可训练的元表示,分别为$c_{pos}, c_{neg} \in \mathcal{D}^k$。$l_{pos}, l_{neg}$这两个类的对数是通过对每个词和相反的元嵌入之间的庞加莱距离求和得到的:

因为我们知道这两个类是相互对立的,我们也考虑为两个元嵌入分配固定的位置。对于欧几里得元嵌入,我们在实验中使用$c_{pos} =(1/\sqrt{k})·1$和$c_{neg} = - c_{pos}$,其中$k$为空间维度。对于庞加莱元嵌入,$cpos = exp_0((1/ \sqrt{k})·1)$和$c_{neg} = - c_{pos}$。
对于训练,我们使用Softmax后的交叉熵作为损失函数。欧几里得探头采用模拟方法。我们对庞加莱球中的所有可训练参数使用RiemannianAdam (Becigneul & Ganea, 2019),特别是两个元嵌入,而对欧几里得参数使用vanilla Adam。
5.1 WORD POLARITIES BASED ON GEOMETRIC DISTANCES
表2报告了分类精度。首先,两种探针都比BiLSTM分类器具有更好的准确率,这意味着上下文化嵌入中存在丰富的情感信息。我们注意到,当修复类元表示时,欧几里得探测会很大有的性能损失,而庞加莱探测甚至可以表现得更好。这一观察结果强烈表明,情绪信息可能以某种特殊的几何方式编码。我们还报告了表3中两个元嵌入之间的距离差距排名最高的情感词,并看到庞加莱探针恢复的词更符合人类直觉(彩色词)。更全面的词表见附录B。各BERT层的分类结果如图5C所示。情感出现在更深的层次(大约第9层),而不是语法(大约第7层,与图2A相比),这就证明了众所周知的假设,即语法是语义的支架。


5.2 VISUALIZATION AND LEXICALLY-CONTROLLED CONTEXTUALIZATION
图5说明了句子是如何嵌入到这两个空格中的。我们看到:
(a)两个探针都区分了非常细粒度的单词情绪,因为人们可以推断出每个单词是积极的、消极的还是中性的,即使探针是在句子级二元标签上训练的;
(b)庞加莱探针比欧几里得探针更清楚地分离了两个元嵌入,并给出了更紧凑的嵌入。
我们强调,图5中的观察结果代表了一般模式,而不是特殊情况。更多的可视化可以在附录B中找到。

为了了解不同的语境化如何改变嵌入的定位,我们仔细地改变了输入词来控制情绪。如图6所示,我们看到:
(a)情绪影响定位:更强烈的情绪会导致与元嵌入的距离更近(子图A v.s. B);
(b)语境化影响局部化:当句子情绪变为否定时(子图A v.s. D),即使这种变化是由简单的否定引起的(子图A v.s. C),所有的词都会更接近否定嵌入。

我们进一步研究了更复杂的情况,探索BERT嵌入的极限(图7),发现:
(a) BERT无法表达双重否定(子图B),这表明双重否定背后的逻辑推理可能对BERT具有挑战性;
(b) BERT对歧义句子给出了合理的定位(子图C),因为大多数单词并不明显更接近一个元嵌入(虚线);
(c) BERT对含有讽刺的句子给出了正确的定位(子图D)。

更多的例子可以在附录B中找到。我们进一步鼓励读者在补充材料中运行Jupyter Notebook,以发现更多的可视化结果。
6 CONCLUSION
本文提出庞加莱探针,可恢复BERT编码的层次信息的双曲子空间。本文的探索为双曲空间中BERT嵌入的几何形状提出了新的分析工具和建模可能性,并详细讨论了树结构、局部化及其与语境化的交互。
